Давным-давно, когда письменные источники научных сведений существовали в единичных экземплярах и тиражировались вручную писцами в монастырях под неусыпным присмотром отцов-настоятелей, контролировать распространение недостоверных знаний было легко и просто. В наше время доступность и безграничность Интернета привели к тому, что справиться с распространением недостоверных данных и массово тиражируемых заблуждений иногда представляется практически невозможным Разыскивая нужную информацию на специализированных сайтах и участвуя в дискуссиях на профильных форумах, порой поневоле задумываешься о создании своего рода информационного Ку-Клукс-Клана — который бы отделял точную информацию от сомнительной и неутомимо и яростно преследовал бы тех, кто бездумно использует комбинации клавиш «CTRL+C»/«CTRL+V» без какой-либо проверки достоверности тиражируемого текста. Сегодня мы поговорим о баллистике нарезного оружия. Пандемия «Copy/Paste», увы, не обошла и эту область — что особенно досадно в настоящее время, когда интерес к нарезному оружию и стрельбе из него в украинском обществе постоянно растет. Рассматривая наш журнал как своего рода маяк, свет которого, указывая судоходный фарватер, не дает кораблям разбиться о скалы, мы попытаемся — без претензий на излишнюю академичность — направить пытливые умы желающих выяснить реальное положение дел в нужное русло. Возможно, для этого кое-какие общепринятые мнения придется уточнить, какие-то — исправить, а какие-то — и вовсе опровергнуть.
Сквозь ствол
Все прекрасно знают, как происходит выстрел: палец стрелка нажимает на спусковой крючок, ударник разбивает капсюль, пороховой заряд сгорает, и давление газов проталкивает пулю через канал ствола, с большой скоростью выбрасывая ее наружу в направлении цели. Многие даже знают, как важны для точной стрельбы идеальные конфигурация и состояние пульного входа, за что отвечает дульная корона, и почему свободно вывешенные стволы значительно круче прочих, таковыми не являющихся — так что все это мы пропустим. Сконцентрируем внимание на том элементе канала ствола, который имеет наиболее важное значение, и о котором одновременно сложено наибольшее количество мифов. Я говорю о нарезах. Для чего каналу ствола нужна винтовая нарезка? Чтобы ответить на этот вопрос, нужно обратиться к пуле. Когда-то ружейные пули имели шарообразную форму, но эти времена давно прошли; нынешние пули — все как одна продолговатые и обтекаемые. В случае с круглой пулей совершенно неважно, какой стороной она прилетит в цель — у шарика все концы одинаковые. В случае вытянутой пули, очевидно, чрезвычайно важно, чтобы она летела носом вперед — иначе в таком дизайне не будет никакого смысла. В полете на пулю действуют силы сопротивления. Как мы помним (о’кей, давайте притворимся, будто помним это) из школьного курса физики, все силы, действующие на тело, можно заменить одной — так называемой равнодействующей, — приложенной в определенной точке. В баллистике и аэродинамике точка приложения совокупной силы к летящему телу называется центром давления. Поскольку силы аэродинамического сопротивления препятствуют полету пули и действуют на ту ее часть, которой она летит вперед (проще говоря, на носовую), то этот центр давления у пули также сдвинут несколько вперед. На самом деле это не проблема. Проблема — то, что из-за этого сдвига центр давления (он же точка приложения результирующей силы сопротивления) оказывается впереди центра масс пули. Те, кто в изучении физики не ограничился школьным курсом, уже знают, что я сейчас скажу. Да-да, из-за этого рассогласования (представляющего собой не что иное, как плечо действия силы) возникает момент. Будь центр давления позади центра масс, этот момент был бы нам на руку, поскольку помогал бы все время направлять пулю носом в сторону цели — так, как это происходит, например, у воланчика для бадминтона, у стрелы, выпущенной из лука, или у моей любимой гладкоствольной пули Бреннеке, к массивному свинцовому телу которой сзади привинчен легкий хвостовик-стабилизатор. Однако в случае, когда центр давления находится впереди центра масс, этот момент становится опрокидывающим. И для того, чтобы пуля не сбилась с курса и поразила цель, этот момент непременно нужно обуздать. Для укрощения опрокидывающего момента и предназначены нарезы. Пройдя по ним, пуля — в придачу к поступательному движению, обусловленному давлением пороховых газов, — приобретает еще и вращательное движение. Вращательное движение массивного тела помогает сохранять положение оси вращения неизменным (именно так ведет себя детский волчок). Таким образом, если пуля вращается вокруг своей оси достаточно энергично, то она сможет побороть опрокидывающее действие сил аэродинамического сопротивления. В этом случае говорят, что пуля обладает гироскопической стабильностью. Но это еще не все. Действие сил аэродинамического сопротивления приводит к тому, что скорость пули постоянно уменьшается — это общеизвестно. Интересно, что все почему-то забывают, что линейная скорость полета пули падает гораздо быстрее, чем угловая скорость ее вращения. Снижение линейной скорости пули приводит к уменьшению величины аэродинамического сопротивления ее полету — и, соответственно, к уменьшению величины опрокидывающего момента; однако вращательное движение пули при этом остается практически неизменным. Вы уже, должно быть, догадались. Вот именно — гироскопическая стабильность винтовочной пули по мере удаления ее от стрелка и приближения к цели не уменьшается, а растет. Проще говоря: нужно добиться, чтобы пуля была гироскопически стабильной в момент ее выхода за дульный срез ствола; а дальше все произойдет само собой.
Чья возьмет?
Как узнать, будет покидающая ствол пуля гироскопически стабильна или нет? Хвала богам, это можно рассчитать заранее.
Для облегчения понимания практического смысла гиростабилизации в частности и жизни энтузиастов стрельбы из нарезного оружия вообще было введено понятие фактора гироскопической стабильности пули (далее — ФГС; в англоя зычных источниках эта же величина обычно обозначается SG или Sg). ФГС очень наглядно иллюстрирует, какое из двух начал победит — светлое, то есть стабилизация пули за счет ее вращения вокруг оси, или темное, то есть опрокидывающий момент. Фактически ФГС равен отношению запаса гиростабильности пули к величине опрокидывающего момента. Если ФГС больше единицы, то это означает, что гиростабильность сильнее, и ваша пуля полетит, как ей и положено. Если ФГС меньше единицы — то попасть этой пулей в цель вам, похоже, не суждено.
Кто в команде?
От чего зависит значение ФГС? Что ж, давайте поразмыслим. Поскольку речь идет о стабилизации вращением — то, очевидно, важную роль имеет угловая скорость вращения пули в момент вылета из ствола. Измерить приборами скорость вращения пули довольно сложно (лично я даже не уверен, что подобные приборы существуют), однако ее не так уж сложно рассчитать — на основе измеренной дульной скорости пули и известной длины отрезка, который нужен пуле для полного оборота вокруг оси (шага нарезов, Господи). По-видимому, играет также роль то, как долго эта угловая скорость вращения способна сохраняться на должном уровне. Любители физики знают, что за сохранение движения, иначе говоря — инерционность, отвечает масса тела; но это — при поступательном движении. При вращении же инерционность
определяется величиной момента инерции. Момент инерции при вращении тела вокруг оси характеризуется распределением масс в этом теле и равен сумме произведений всех элементарных масс, составляющих тело, на квадрат расстояния от этих элементарных масс до оси вращения. Это означает, что величина момента инерции (или то, насколько хорошо и долго вращающееся тело способно сохранить свое вращательное движение) определяется не только — и не столько — общей массой тела, но еще и его размерами и формой. Причем размеры и форма, пожалуй, «рулят» сильнее, чем масса — неслучайно же упоминался квадрат расстояния, а не первая степень. Сведущие в механике и механизмах могут вспомнить такое устройство, как маховик. Как все знают, чем массивнее маховик, тем дольше он сохраняет вращение. Однако вспомните, случалось ли вам видеть маховик, который бы имел форму не диска с диаметром, значительно превышающим его толщину, а, например, круглого стержня? Или тот же детский волчок, который легко можно было сделать самому без помощи мамы или папы — всего-то и нужно было, что кружок из толстого картона и более-менее длинный ровный гвоздик. Вот только если этот картонный кружок заменяли, скажем, пластилиновым шариком, то волчок почему-то устойчиво вертеться отказывался. Что ж, теперь вы знаете почему. Итак, у нас есть дульная скорость, шаг нарезов, масса пули, ее длина и диаметр. Что еще? По-видимому, важна также и форма пули — ведь она во многом определяет, как сильно проявляется аэ родинамическое сопротивление при ее полете (что-то подсказывает, что форму пули удастся выразить каким-нибудь коэффициентом). И наверняка не обойтись без данных о метеоусловиях — температуре воздуха, давлении и влажности.
Два пишем, три в уме
Математические методики и формулы, позволяющие увязать вместе все эти данные, известны баллистикам не год, не два и даже не сто. Наверняка вам где-нибудь встречалось такое словосочетание, как «формула Гринхилла» — еще в 1879 г. ее вывел, натурально, сэр Альфред Джордж Гринхилл, профессор математики из британской Королевской военной академии. Формула сэра Альфреда связывала необходимую крутизну нарезов ствола с калибром пули и ее длиной; присутствовали также и поправочные коэффициенты — пусть грубо, но все же учитывающие скорость пули и ее конструкцию (именно конструкцию, а вовсе не форму). Формула Гринхилла, пусть не сразу, но все же получила признание: в 1929 г., уже после смерти автора, она была включена в Британский справочник по стрелковому оружию. Несмотря на то, что формула Гринхилла была достаточно грамотно обоснована, хороша она была только для представлений о пулях и их движении, сложившихся на момент ее создания, то есть к концу XIX века. Поэтому
попытки ее улучшить (упростить, одновременно сделав более точной) не прекращались. Известен результат работы специалистов по баллистике компании Sierra Bullets, основанной в 1947 г. в штате Калифорния, США (в 1990 г. компания перебралась в г. Седалиа, штат Миссури). Скрупулезность и дотошность инженеров этой фирмы не вызывают никаких сомнений: неслучайно пули Sierra Bullets до сих пор являются эталоном того, какими должны быть винтовочные пули — хоть охотничьи, хоть спортивные. Формула компании Sierra Bullets была значительно проще исходной британской формулы, а также точнее — поскольку учитывала уже и начальную скорость пули. И, наконец, в 2005 г. случился очередной прорыв. Взяв за основу формулу Гринхилла и отталкиваясь от современных знаний об аэ родинамике, американский математик Дон Миллер вывел формулу, ныне известную как правило крутизны нарезов Миллера (англ. Miller Twist Rule). В выражении для расчета ФГС она выглядит так: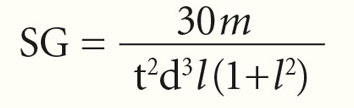 
где SG — значение фактора гироскопической стабильности (ФГС), m — масса пули (в гранах), d — калибр пули (в дюймах), t — шаг нарезов (в калибрах), l — длина пули (в калибрах). Обратите внимание: масса пули в формуле Миллера стоит в числителе. Таким образом, при росте массы пули значение ее фактора гироскопической стабильности также растет. Запомним это. Число «30» в числителе взято вовсе не с потолка — это константа, характеризующая скорость пули и соответствующая начальной скорости, равной 2800 фут/с; если реальная скорость не равна этому значению, вводится дополнительный поправочный коэффициент, который вычисляется по формуле: 
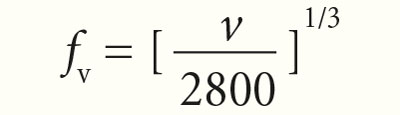Как видно, с ростом скорости значение этого поправочного множителя (а следовательно, и значение ФГС) также увеличивается. Что касается метеоусловий, то формула Миллера справедлива для их значений, соответствующих нормативу U.S. Army Standard Metro (температура воздуха 59 oF/15 oC, атмосферное давление 750 мм рт. ст., относительная влажность 78%). В случае, если реальные мете оусловия будут иными, используется дополнительный поправочный коэффициент. Как видим, формула Дона Миллера учитывает все характеристики движения пули, которые мы насчитали.
Шпаргалки баллистических двоечников
Формулы всем хороши, кроме одного — искомые значения они высчитывают по одному за раз. Именно поэтому и школьники, и студенты вузов во все времена использовали, используют и будут использовать шпаргалки. Шпаргалка не требует глубинных знаний предмета и вдобавок позволяет действовать крайне оперативно. Однако если для разбирающегося в предмете ошибка при переписывании формул некритична, поскольку непременно будет замечена и исправлена при дальнейших расчетах, то неточность в составлении шпаргалки гарантированно обеспечит воспользовавшемуся ей двоечнику провал на экзамене. Нечто подобное и произошло благодаря приведенной здесь таблице. Ее автор, известный американский производитель
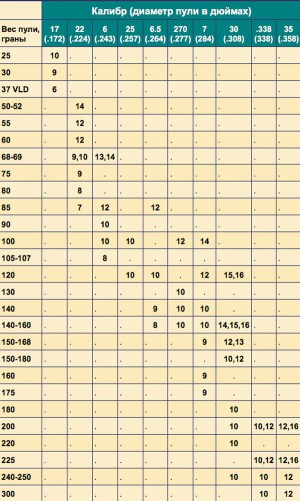
штучных высокоточных стволов Дэниел Лилья, при составлении наверняка преследовал исключительно благие цели — по-видимому, намереваясь до предела упростить жизнь своим кли ентам при заказе новых стволов. В таблице Лильи массе пули и ее калибру ставилось в соответствие значение шага нарезов ствола — при этом ни длина пули, ни ее скорость в расчет не брались. Нет никаких сомнений, что сам Дэниел Лилья, высококвалифицированный инженер-ствольщик, прекрасно знал о важности и весомости этих характеристик. Представляется, что его таблица была составлена вовсе не для использования в качестве отправной точки при баллистических расчетах — а исключительно для того, чтобы потенциальный клиент, заказывая штучный ствол на свой серийный «Ремингтон» или «Сэведж», мог сориентироваться, какой шаг нарезов ему указать в заказе, исходя из предпочитаемого типа пуль. Впрочем, на всякий случай в комментариях к таблице (оригинал здесь — riflebarrels.com/calibers-and-twist-rates) Лилья указал, что данные из таблицы справедливы для оболочечных пуль со свинцовым сердечником — а в случае же, например, монолитных пуль из меди и латуни и пуль с пластиковым баллистическим наконечником таблица может не сработать, поскольку такие пули при той же массе будут значительно длиннее. Возможно, комментарии Лильи заставили бы кого-то задуматься — вот только в русскоязычный Интернет его таблица перекочевала уже без каких-либо уточнений. И поскольку таблица Лильи была русифицирована (полученный в результате документ лично я называю Таблицей-обманкой) задолго до того, как на постсоветском пространстве стала доступна услуга замены родных стволов фабричных винтовок на штучные — вполне естественно, что использовать ее стали не для подбора оптимального твиста под имеющуюся пулю, а для выбора пуль под шаг нарезов имеющегося оружия.
Порвать и выкинуть. А лучше изначально не прикасаться
Чем же на практике плоха или вредна Таблица-обманка, и почему при серьезном подходе к делу следует игнорировать все подобные таблицы, а пользоваться исключительно формулой? То, что в Таблице-обманке не учитываются ни длина пули, ни ее начальная скорость, мы уже упоминали; но это звучит слишком уж абстрактно и не дает всей полноты картины. Душа требует примеров, расчетов и картинок. Извольте.
Длина пули. Знакомство с ассортиментом серийно выпускающихся в настоящее время винтовочных пуль свидетельствует, что их длины и массы отнюдь не всегда пропорциональны друг другу. В рамках одного и того же калибра более тяжелая пуля может быть как короче какой-нибудь более легкой, так и длиннее — все зависит от форм конкретных пуль, их конструкций и материалов, из которых они изготовлены. При заданной массе и одном и том же калибре самой короткой, очевидно, будет цельносвинцовая безоболочечная пуля-цилиндр. Введение в конструкцию медной либо латунной оболочки приведет к увеличению длины пули, изменение тупоконечной формы носовой части на более обтекаемую — к еще большему увеличению. Полость в носовой части удлинит пулю еще больше, закрывающий эту полость заостренный пластиковый наконечник сделает ее еще длиннее; в случае же пуль, целиком изготовленных из более легкого, чем свинец, материала (например, медного сплава) длина их увеличивается чуть ли не в разы. К чему это приводит? Как видно из формулы Миллера, при прочих равных с ростом длины пули значение ФГС падает. В таблице же каждой паре «калибр пули/твист» соответствует некое значение «разрешенной» массы. Первая опасность в этом случае: вы можете выбрать пулю, вроде бы подходящую по массе, однако слишком длинную — и в итоге получить недостаточную гиростабилизацию. Вторая опасность: вы можете необдуманно отказаться от пули большей массы (тем самым потеряв обеспечиваемые ею возможности) — которая, тем не менее, прекрасно бы стабилизировалась в вашем стволе 
благодаря умеренной длине. Скорость. Калибр пули никак не связан с мощностью патрона; например, одной и той же пулей Hornady SP 165 гран .30-го калибра можно снарядить как патрон .300 AAC Blackout, так и патрон .30-378 Weatherby — при этом скорость пули будет отличаться чуть ли не в разы. Вдобавок как скорость пули сама по себе, так и значение ФГС уменьшаются с понижением температуры воздуха — вполне может случиться так, что патрон, пуля которого прекрасно стабилизировалась летом, совершенно непригоден морозной зимой. Формула Миллера это учитывает. Таблица-обманка — нет. Теперь, когда все мы уже достаточно напуганы, следует объявить, что решение существует — и перейти к его описанию.
Порядок действий
Вести расчеты с помощью формулы Миллера не так уж и сложно. Тем более что этот процесс, в сущности, давно механизирован — я пока об этом помалкивал, чтобы нагнать побольше ажиотажа. Одним из наиболее знаменитых и уважаемых производителей пуль для высокоточной стрельбы (причем не только стрельбы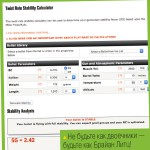 
по мишеням, но и по охотничьим целям тоже) является компания Berger. В Украине ее продукция — знаменитые пули VLD, HPBT Long Range, Hybrid и другие — представлена уже несколько лет; в странах же, где нарезное оружие распространено значительно больше, пули Berger давно считаются наилучшими. Однако не только этими пулями славится компания Berger — определенную и очень значительную долю почета и признания в мировом стрелковом сообществе фирме принес ее штатный баллистик Брайан Литц. Можно долго описывать важность исследований, уже проведенных и проводимых в настоящее время
Брайаном Литцем, и перечислять опубликованные им книги по современной баллистике, однако объем нашей статьи ограничен; поэтому скажем коротко и ясно: Брайан Литц в баллистике имеет примерно тот же статус, что сэр Пол Маккартни — в музыке (если же вам ближе визуальное восприятие, то пусть будет Пьер Вудман). Именно благодаря работе Брайана Литца справочные материалы на сайте Bergerbullets. сom представляют собой поистине энциклопедические издания. И это еще не все: по-видимому, именно с подачи Брайана Литца на сайте компании Berger теперь есть простой и понятный онлайн-калькулятор фактора гироскопической стабилизации пуль (bergerbullets.com/twist-rate-calculator). Вот и все — вам больше не нужно вручную высчитывать на калькуляторе сначала нормированное
значение ФГС для вашей пули и винтовки, а потом все необходимые поправочные коэффициенты. Просто откройте страницу сайта, озаглавленную Twist Rate Stability Calculator, введите в нужные поля требуемые значения (а если в расчетах участвует какая-нибудь из пуль компании, то и вводить не нужно — ее можно выбрать в выпадающем списке), кликните «мышкой» на кнопке Calculate Stability — и вот он, искомый ФГС. Единственная трудность может возникнуть, если при проведении расчетов у вас еще нет пуль, которые вы намерены запускать из вашей винтовки — то есть если их длина вам неизвестна. Эта проблема тоже легко решается — можно воспользоваться данными, опубликованными на сайте JBM Ballistics (jbmballistics.com/ballistics/lengths/lengths.shtml). Значения длин пуль, приведенные там, иногда слегка завышены, но это не беда — если выяснится, что ФГС для табличного значения вас устраивает, то результат для чуть меньшей фактической длины устроит тем более.
Трактовка результатов и некоторые практические примеры
Обратите внимание на диаграмму, расположенную ниже расчетной формы (для большей понятности мы приводим русскоязычный вариант). Задача этой диаграммы — помочь вам понять, что именно означает то или иное полученное при расчетах значение ФГС.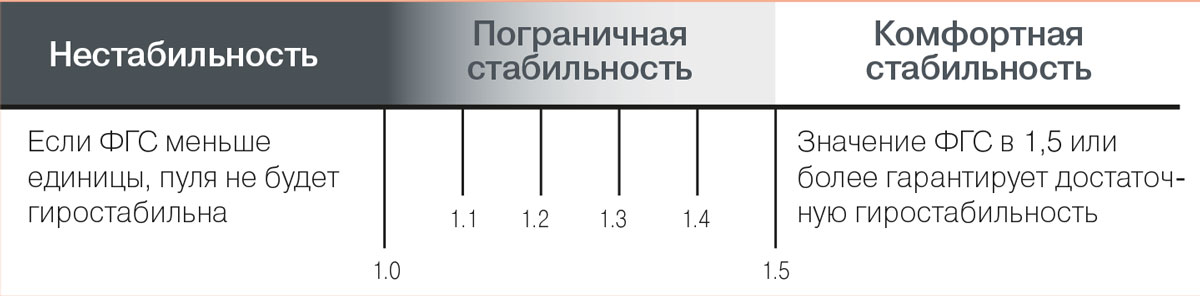 
Как уже упоминалось, ФГС должен быть больше единицы — это непременное условие для того, чтобы ваша пуля не летела кувырком. С этим понятно — но насколько больше единицы должен быть ФГС? Или: насколько больше единицы он МОЖЕТ быть? В своей книге «Прикладная баллистика при стрельбе на большие расстояния» Брайан Литц указывает, что значение ФГС должно превышать единицу с некоторым запасом «на всякий пожарный случай» — и составлять не менее 1,4. Также он отмечает, что стрелки бенчрест-дисциплин, которые собирают патроны чуть ли не непосредственно перед стрельбой зачетной серии (точно учитывая текущие метеоусловия — которые, как правило, и являются причиной «пожара»), стараются поддерживать значение ФГС для своих пуль на уровне примерно 1,3. Основываясь на определенной статистике, лично я считаю, что эти значения больше применимы для стрельбы по бумажным мишеням. По всей видимости, при стрельбе по целям, которые пуле придется пробивать, углубляясь в них достаточно существенно — например, при стрельбе по дичи на охоте — запас в стабилизации будет, скорее, полезен, чем вреден. Опять же, нужно учитывать, что стрельба на охоте обычно происходит при минусовых температурах, из-за чего значение ФГС снижается. В русскоязычном стрелковом интернет-сообществе бытует твердое мнение, что при ФГС, превышающем значение 1,5, наступает нечто, что они называют «перестабилизацией пуль». Часть этого сообщества (как свидетельствует статистика, основной процент этой части составляют спортсмены, занимающиеся динамическими видами стрельбы) уверена, что именно перестабилизация виновна в ухудшении кучности стрельбы. В качестве подтверждения истинности логических построений неизменно приводится ссылка на Таблицу-обманку (большинство динамических стрелков, хотя не только они, вообще не заморачиваются какими-либо измерениями или вычислениями, сразу апеллируя к вышеупомянутой таблице). Так ли это, и действительно ли нужно бояться этой самой «перестабилизации», то есть превышения ФГС значения 1,5? Что ж, давайте посмотрим на диаграмму. Отметка «1,5» на ней действительно выделена — она отмечает окончание диапазона «Пограничная стабильность» (начинался это диапазон с единицы) и начало области «Комфортная стабильность». При этом верхняя (правая) граница области «Комфортной стабильности» на диаграмме не отмечена — ее попросту нет, — а комментарий внизу говорит лишь, что «значение ФГС в 1,5 или более гарантирует достаточную стабильность». И я лично почему-то далек от мысли, что Брайан Литц понимает в стабилизации пуль меньше, чем участники русскоязычных интернет-форумов. На всякий случай приведем ряд примеров:
— пуля Hornady BTHP Match 52 грана калибра .224 на дальности 100 м демонстрирует кучность в районе 0,5 МОА и менее из винтовок типа AR-15 калибра .223 Rem с твистом 1:9” (ФГС — 2,36); — пуля Hornady V-Max 53 грана этого же калибра, значительно более длинная, чем предыдущая, демонстрирует такую же кучность из того же оружия (ФГС — 1,64), однако отказывается стабилизироваться из стволов с твистами 1:14” и 1:12” (в обоих случаях ФГС — меньше единицы); — пуля Prvi Partizan SP 150 гран, выпущенная из винтовки калибра .308 Win с твистом 1:10”, способна демонстрировать субминутную — точнее, 0,910 МОА, — кучность на 100 м (ФГС – 3,21); — из зарубежного опыта (наш читатель из Филадельфии, штат Пенсильвания, США): группа из пяти пробоин пулей Sierra Varminter 110 гран .30-го калибра, разогнанной из винтовки калибра .308 Win с твистом 1:12” до скорости около 3100 фут/с (ФГС — 3,89), на дальности 100 ярдов полностью накрывается 10-центовой монеткой (диаметр — 0,705”). Теперь зайдем с другого фланга. Как искренне считают поклонники Таблицы-обманки, там приведены предельные значения масс пуль, которые может стабилизировать отмеченный твист — и если в этом же калибре взять пулю большей массы, то ее указанный твист, что называется, «не потянет». Что на это ответят формула Миллера и онлайн-калькулятор Литца? С формулой все понятно — как помните, масса там стоит в числителе, и ФГС с ростом массы тоже увеличивается. Онлайн-калькулятор это подтверждает. При этом варьирование начальной скоростью, как мы помним, в целом сказывается на значении ФГС — но не так, чтобы очень. Получается, что нужно остерегаться вовсе не прироста массы пули — а исключительно увеличения ее длины. Тут тоже не обойтись без примеров: — охотничья пуля Sierra ProHunter 220 гран .30-го калибра, как выясняется, прекрасно стабилизируется в стволе винтовки калибра .308 Win с твистом 1:12” — несмотря на холодный отрыв, кучность тестовой группы из пяти выстрелов на дальность 100 м составила 1,255 МОА, и все пробоины вышли идеально круглыми, что свидетельствует о полной стабилизации (ФГС — 1,67); — спортивная пуля Hornady BTHP Match 208 гран того же калибра, несмотря на чуть меньшую массу и существенно большую длину, достаточно стабильна из того же оружия — кучность 0,539 МОА (ФГС — 1,10). [toggle status=opened title=»Таблицы»] На десерт мы приготовили несколько таблиц, в которых приведены данные реально существующих фабричных патронов – еще раз подтверждающие превосходство формул над шпаргалками, когда нужен точный ответ. Обратите внимание: — малая масса пули может не так уж и хорошо работать с пологим твистом, если она сопровождается большой длиной (таблицы I и II); — большая масса – не помеха стабилизации, если длина пули сохраняется в разумных пределах (таблицы II и III); — в калибре .223 Rem армейский твист 1:7” для пуль коммерческого образца совершенно не нужен (таблица I). Заметьте – это еще не все выводы. Развлекайтесь ? Таблица 1. Значения ФГС фабричных патронов Black Hills калибра .223 Rem»]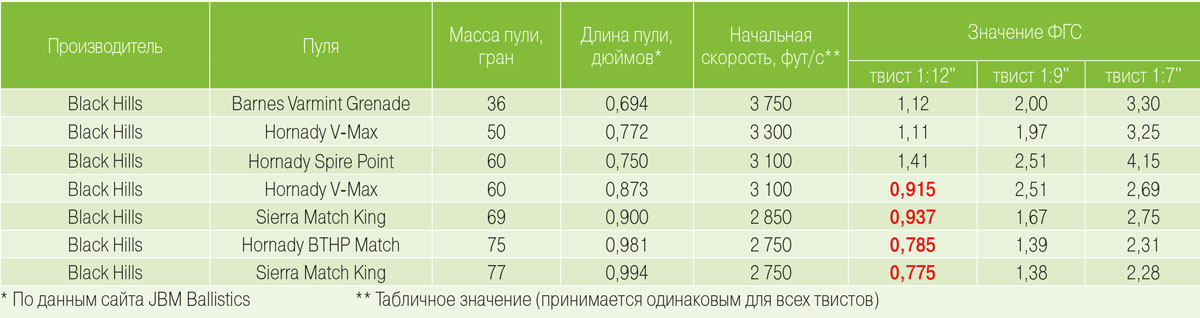
Таблица 2. Зависимость ФГС от температуры для патронов калибра .308 Win (твист 1 1:12″)»]
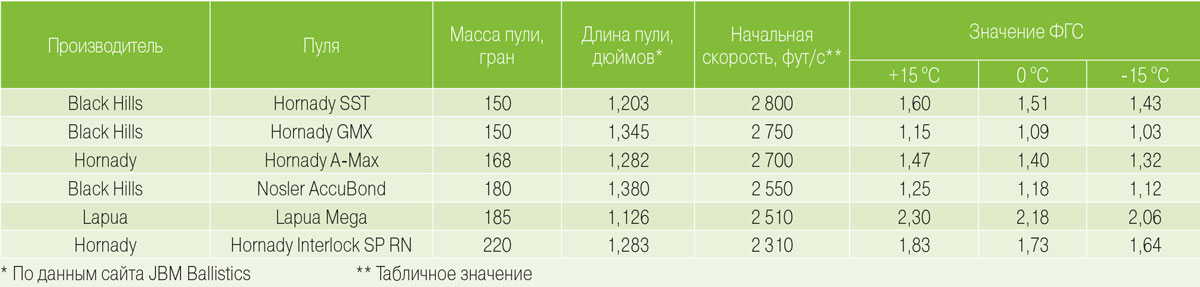«Таблица 3. Значения ФГС некоторых дозвуковых патронов. 30-го калибра»]
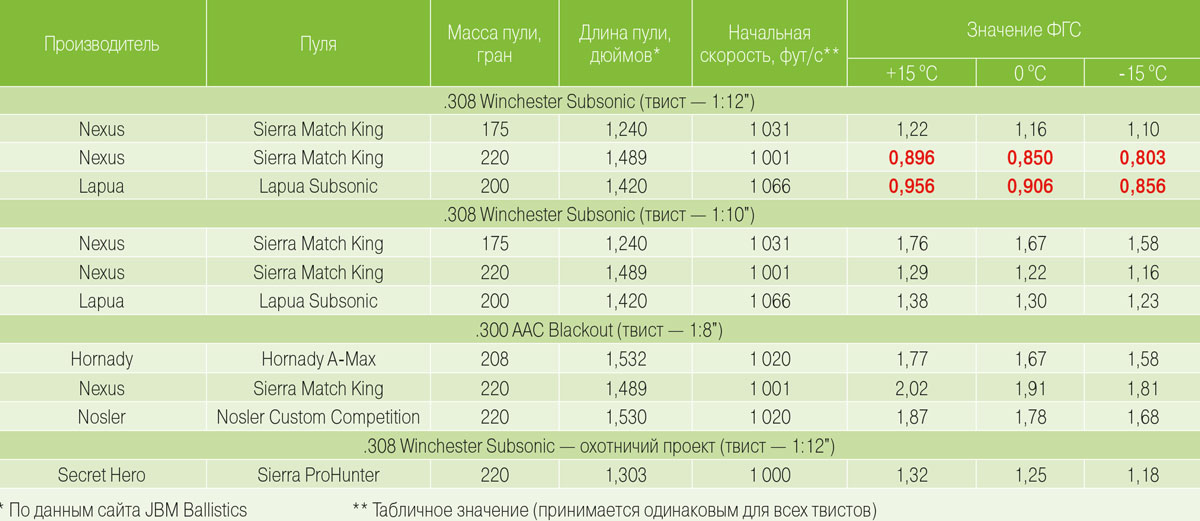[/toggle]
Как вы пулю назовете…
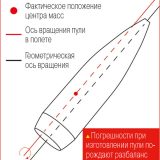
В каких же случаях повышенное значение ФГС может навредить (если, конечно, такое может случиться)? Увы, может. Правда, тут дело вовсе не в чрезмерной стабилизации пуль, а всего лишь в увеличенной угловой скорости их вращения. А также в качестве изготовления самих пуль. Здесь, кстати, нам следует принести извинения поклонникам динамических видов стрельбы. Дело в том, что винтовочные пули обычно имеют неоднородную конструкцию. Чаще всего они состоят из оболочки, латунной
или биметаллической, и запрессованного в нее свинцового сердечника (конструкцию армейских пуль, у которых внутри свинцового сердечника обычно размещается еще и стальной, мы рассматривать не будем). Оболочка пуль обычно имеет вырезы с носовой либо кормовой стороны, свинцовый сердечник может иметь пустоты, а также оснащаться разнообразными вставками (например, для реализации экспансивного действия). Сложность конструкции приводит к тому, что при любых погрешностях, допущенных при изготовлении того или иного элемента пули, ее суммарный центр масс сдвигается в сторону от ее геометрической оси симметрии. При движении пули по стволу это не слишком страшно — у нее нет других вариантов, вокруг чего вращаться, поскольку она ограничена в маневре стенками канала ствола. Однако при выходе за дульный срез пуля, что называется, «расправляет крылья» — и вне зависимости от того, совпадает там что с чем или нет, начинает вращаться вокруг новой оси, которая теперь проходит через центр масс. А дальше вступает в действие правило, колоритно сформулированное капитаном Врунгелем. Если оболочка пули была изготовлена идеально равностенной, сердечник вышел идеально однородным и симметричным, а его запрессовка в оболочку получилась идеально концентричной, то никакого разбаланса при выходе пули в «свободный полет» не произойдет. Идеально точно, конечно, серийную пулю сделать не получается — даже мастера-штучники, изготавливающие пули вручную, обычно работают по принципу «из тысячи полученных отбираем полсотни лучших, а остальные — в переплавку». Поэтому разбаланс в той или иной степени всегда имеет место. Именно ощутимый разбаланс является основной причиной, почему некоторые пули подвержены повышенному рассеиванию при стрельбе. Эмпирически доказано, что с увеличением угловой скорости вращения пуль разбаланс проявляется сильнее, и рассеивание пуль растет. Очевидно, что при минимально возможной величине разбаланса влияние крутого твиста, резко увеличивающего угловую скорость вращения пуль, проявляется не так сильно — а в некоторых случаях может быть вообще незаметно для стрелка. Именно поэтому пули матчевого класса — например, Sierra MatchKing, Hornady BTHP Match и A-Max, Lapua Scenar, Nosler Custom Competition и практически весь модельный ряд пуль Berger (эта контора не-матчевых пуль, похоже, вообще не делает) — совершенно наплевательски относятся к увеличению крутизны твиста. Хотя, конечно, намеренно увеличивать угловую скорость, пихая в ствол с крутым твистом более короткие пули, нет никакого смысла. Зато если пули изначально были сделаны не очень качественно, то разбаланс вследствие увеличенной крутизны твиста проявится на полную катушку. Именно из-за этого и страдают любители динамической стрельбы. Характерное для этих непреклонных людей категорическое утверждение «в .223- м калибре легкие пули из крутых твистов не летают!», как показывает дознание, обычно означает, что из чьей-то Norinco c хромированным стволом (что само по себе противоречит понятию «кучность») патрон Wolf/TulAmmo с пулей массой 62 грана демонстрирует чуть лучшую кучность, чем такой же патрон с пулей массой 55 гран. Нежелание выстрелить хотя бы для пробы фабричными патронами принципиально более высокого качества, снаряженными легкими матчевыми пулями либо пулями варминт-типа (их точность обычно крайне незначительно уступает матчевым, если вообще уступает) — например, патронами Black Hills Gold с пулями Hornady V-Max либо Federal с пулями Nosler BallisticTip — динамические стрелки объясняют нежеланием проводить эксперимент ради самого эксперимента. Ведь при любом его исходе принципиально более высокая цена качественных импортных патронов делает их приобретение даже по оптовым ценам неподъемным для стрелков динамических дисциплин, ведь расход боеприпасов за одну тренировку у этих спортсменов превышает чуть ли не месячную норму настрела высокоточников, а охотникам этого запаса хватило бы вообще на два или три сезона. Поэтому выхода у «динамических» стрелков нет — и от валовых патронов с пулями в биметаллических оболочках, отштампованных по конверсионным технологиям на оборудовании, один лишь вид которого заставляет навсегда забыть понятия «равностенность» и «концентричность», им, увы, никуда не деться. 
Совсем другое дело, если вы — охотник или стрелок-высокоточник. Не имеет значения, на какую дичь вы охотитесь, или какова дальность до мишеней, самый центр которых вы дырявите — практически для любого калибра, который используется в первом или втором случае, можно подобрать серийную пулю либо просто высокого, либо высочайшего качества. И в том, и в другом случае выигрышные комбинации, скорее всего, будут начинаться со слов Berger, Hornady, Lapua, Nosler или Sierra. Как выбрать из ассортимента этих торговых марок пули, наилучшим образом подходящие к стволу вашей винтовки, вы уже знаете. О выборе из полученных вариантов наилучшего решения с точки зрения условий стрельбы и характеристик обстреливаемой цели вы сможете прочесть в следующих номерах нашего журнала.
